Inverzne trigonometrijske

funkcije
Ako izraz y = sin(x) znači: "x je mera ugla čiji je sinus jednak y" onda izraz y = arcsin x znači: "y je arkussinus onog ugla čiji je sinus jednak x".

Funkcija y = arcsin x se naziva inverzna sinusna funkcija. Dakle, možemo zaključiti da važi:



Primer 1: Ako je π/6 = arcsin(1/2) onda je sin(π/6) = 1/2.

Za preostalih pet elementarnih trigonometrijskih funkcija odgovarajuće inverzne će biti: arccos(x) (čita se "arkus kosinus od x" za cos(x)), arctg(x) ("arkus tangens od x" za tg(x)), arccsc(x) (čita se "arkus kosekans od x" za csc(x)), arcsec(x) ("arkussekans od x" za sec(x)) i arcctg(x) (čita se "arkus kotangens od x" za cot(x)).

Domen funkcije y = arcsin(x)

Pogledajmo najpre koliko iznosi arcsin(0)?
Možemo lako videti da jedna od vrednosti ugla za koju je sinus jednk 0 je vrednost ugla 0. Takođe, arcsin(0) = 2π. Takođe, možemo primetiti da je arcsin(0) = nπ, za n ∈ Z.
Restrikovan domen funkcije y = arcsin(x) iznosi:



A sada pogledajmo �mu je jednak arkussinus negativnog ugla tj. arcsin(-θ)? Pogledajmo sledeću sliku 1.

                Slika 1.
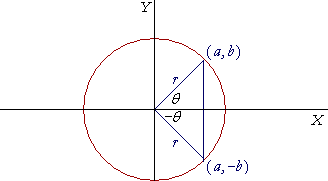
Sa slike možemo videti da je

arcsin(θ) = b/r    i da je

arcsin(- θ) = - b/r .

Možemo zaključiti da je

arcsin(- θ) = - arcsin(θ).
Primer 2: Izračunati arcsin(-1/2).

Neka je arcsin(-1/2) = θ. Tada je sin(θ) = -1/2. Na osnovu ranije priče o znaku sinusa po kvadrantima, znamo da je sinus negativan u četvrtom kvadrantu. Takođe, iz činjenice da je arcsin(-θ) = - arcsin(θ), imamo da je arcsin(-1/2) = - arcsin 1/2 = - π/6.

Domen funkcije y = arctg(x)

Slično kao kod arkussinus funkcije, i domen arkustangensa se može restrikovati i on pripada sledećm intervalu:



Opet kao kod arkussinusa, arkustangens negativnog ugla je negativan.

Dokaz:
Ako opet pogledamo sliku 1. možemo videti da je

arctan(θ) = b/a    i da je

arcsin(- θ) = - b/a, pa iz toga zaključujemo da je

arctg(- θ) = - arctg(θ)

Primer 3: Izračunati arctan(-1/2).

Ako je arctg(-1) = θ, onda je tan(θ) = -1. Znajući da je vrednost tangensa u četvrtom kvadrantu negativna i da je, na osnovu prethodno dokazanog, arctg(- θ) = -arctg(θ), imamo da je arctg(-1) = -arctg(1) = - π/4.

Domen funkcije y = arccos(x)

Ova funkcija je inverzna trigonometrijska funkcija funkciji cos(x) i ona ima najmanju apsolutnu vrednost kada se y kreće u prvom i drugom kvadrantu. Zato je domen ove funkcije interval [0,π]. Dakle:



Ako pogledamo sledeću sliku 2., možemo primetiti da se ugao θ, čiji je kosinus negativan, nalazi u drugom kvadrantu i da je kosinus uglova koji pripadaju drugom kvadrantu jednak negativnom kosinusu uglova koji su suplementni uglovima drugog kvadranta.

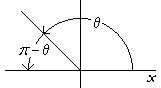
       Slika 2.
Matematički zapisano: arccos(-x) = π - arccos(x).

Primer 4: Izračunati arccos(-1/2).

arccos (-1/2) = π - arccos(1/2) = π - π/3 = 2π/3

Domen funkcije y = arcsec(x) i y = arccsc(x)

Za funkciju y = arcsec(x) domen pripada intervalu 0 < y < π/2 , x > 0. Ako, međutim je x < = 0, tada je domen interval -π < y < π/2.

Za funkciju y = arccsc(x), domen je interval 0 < y < π.






Prethodna ..... Sledeća