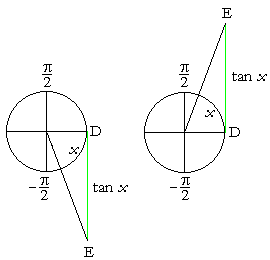
Slika 9.
Zato grafik funkcije za I i IV kvadrant izgleda ovako (slika 10):
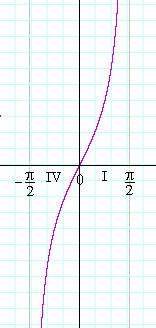
Slika 10.

Slika 1.Prethodni zaključak važi za bilo koji argument funkcije sin(θ). Na primer:
Slika 2.I konačno grafik funkcije y = sin(x) izgleda ovako (slika 3.):
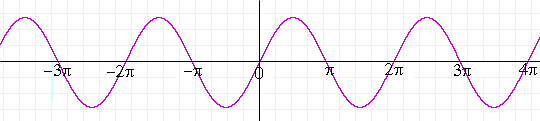
Slika 3.Nezavisno promenljiva x može uzimati bilo koju realnu vrednost.
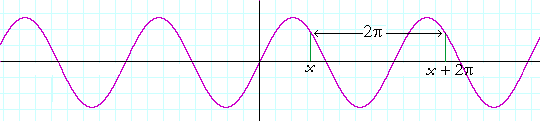
Slika 4.Grafik funkcije y = sin(ax)
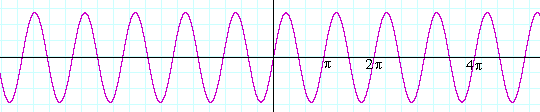
Slika 6.Primer2:
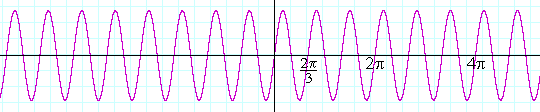
Slika 7.Primer3:
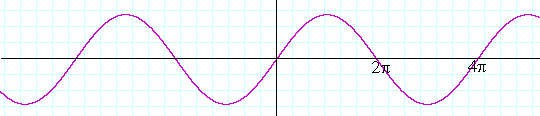
Slika 8.
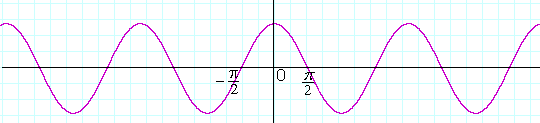
Slika 5.Identitet sin (x + π/2 ) = cos x ćemo dokazati u nekoj od narednih oblasti.

Slika 9. |
Možemo primetiti da kako se x kreće u intervalu (-π/2, π/2), tako tg(x) (čije vrednosti pripadaju duži DE) uzima bilo koju realnu vrednost tj. tg(x) pripada intervalu (-∞, +∞). Zato grafik funkcije za I i IV kvadrant izgleda ovako (slika 10):  Slika 10. |
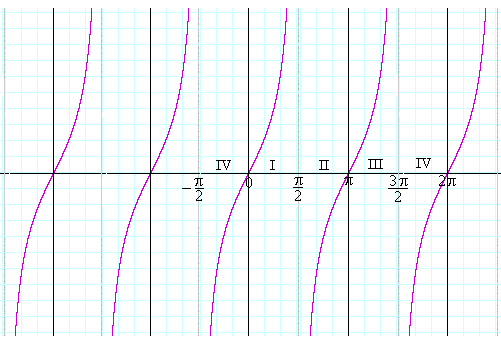
Slika 11.Na kraju, pogledajmo aplet koji interaktivno prikazuje grafike sinusne, kosinusne i tangensne funkcije.