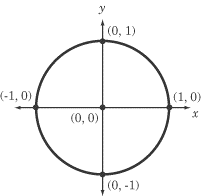
Slika 1.


Slika 1. |
Jedinični krug se x-osu u tačkama (-1,0) i (1,0) i y-osu u tačkama (0,1) i (0,-1). |
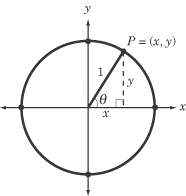
Slika 2. |
Na slici 2. vidimo kako to izgleda. Poluprečnik jediničnog kruga u bilo kojoj tački je hipotenuza pravouglog trougla čija horizontalna kateta je dužine cos(θ) a vertikalna dužine sin(θ). Ugao θ je u standardnom položaju. Na osnovu ranije definicije funkicje sinus i kosinus dobijamo sledeće jednakosti: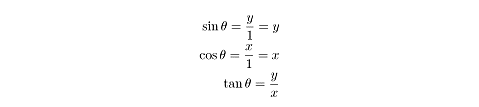 Naravno, x i y su koordinate proizvoljne tačke P na jediničnom krugu tj. normalna rastojanja tačke P od x i y ose. Ta rastojanja su istovremeno jednaka dužinama kateta uočljivog pravouglog trougla sa slike 2. Znajući vrednosti za sin(θ) i cos(θ), lako nalazimo kolika je vrednost funkcije tg(θ). |
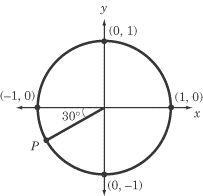
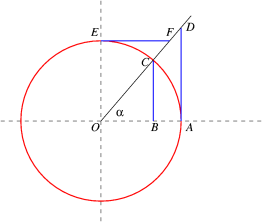
Slika 3. |
Zadatak1: Odrediti koordinate tačke P date na slici 3. Reenje: Tačka P je tačka poluprečnika jediničnog kruga, koji sa negativnim smerom x-ose zaklapa ugao od 30. Taj ugao je jednak uglu od 210, koji zaklapa taj isti poluprečnik ali sa pozitivnim smerom x-ose. Pošto smo u dosadašnjem izlaganju o jediničnom krugu videli kako određujemo koordinate tačke P, kada se ona nalazi na završnom kraku ugla koji je u standardnom položaju, u ovom slučaju koordinate tačke P biti (cos(210), sin(210)) = (√3/2, 1/2). Možemo primetiti da su obe koordinate tačke P negativne, jer se ona nalazi u trećem kvadrantu. |
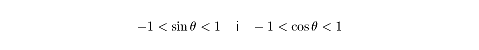
 Slika 4. |
|
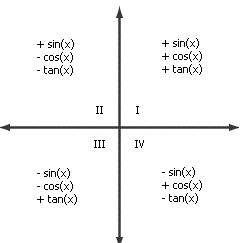
Slika 5.
Slika 6.
|
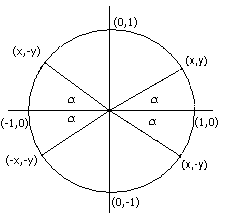
I kvadrant: θ = α sin(θ) = y/1 = y cos(θ) = x/1 = x tan (θ) = y/x II kvadrant: θ = 180-α sin(θ) = sin(180° - α) = y/1 = sin(α) cos(θ) = cos(180° - α) = -x/1 = -cos(α) tan(θ) = tg(180° - α) = -y/x = -tg(α) |
III kvadrant: θ =180 + α sin(θ) = sin(180° + α) = -y/1 = -sin(α) cos(θ) = cos(180° + α) = -x/1 = -cos(α) tg (θ) = tg(180°+ α) = -y/(-x) = y/x = tg(α) IV kvadrant: θ = 360 - α sin(θ) = sin(360° - α) = -y/1 = -sin(α) cos(θ) = cos(360° - α) = x/1 = cos(α) tg(θ) = tg(360° - α) = -y/x = -tg(α) |
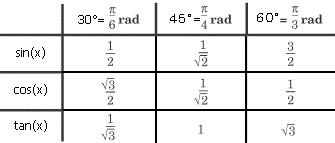
Slika 7.
Slika 8. |
Sa slike možemo videti sledeće: cos(-α) = x/1 = cos(α) sin(-α) = -y/1 = - sin(α) tg(-α) = -y/x = - tg(α) |
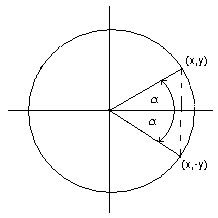
Slika 9. |
Sa slike možemo videti da se nalazi u drugom kvadrantu i da se zato ugao od 120° može zapisati kao 120° = 180° - 60°. Zbog toga je sin(120°) = sin(180° - 60°) = +sin(60°) = √3/2 |
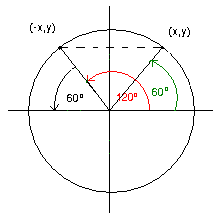
Slika 10. |
Dakle, uz pomoć jediničnog kruga možemo videti da se završni krak traženog ugla nalazi u drugom kvadrantu i da se zato taj ugao može zapisati kao 330° = 360° - 30°. Zbog toga je tg(330°) = tg(360° - 30°) = -tg(30°) = -1/√3 |
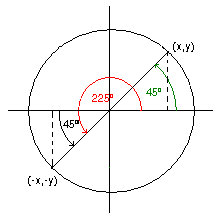
Slika 11. |
Sa slike možemo videti da je cos(225°) = cos(180°+45°) = -cos(45°) = -1/√2 |