Radijan i stepen

Za ugao BAC kažemo da se nalazi u standardnom položaju ako mu je teme (A) na koordinatnom početku u xy-ravni, jedan krak (AB) tog ugla je fiksiran i leži na pozitivnom smeru x-ose a drugi krak (AC) može da rotira (vidite sliku).

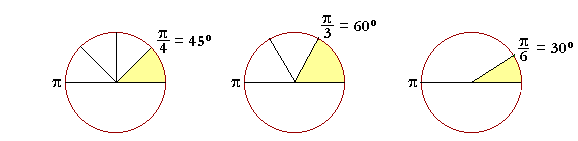
Fiksirani krak AB se naziva inicijalnim krakom, dok se rotirajći krak AC, naziva krajnjim ili završnim krakom.

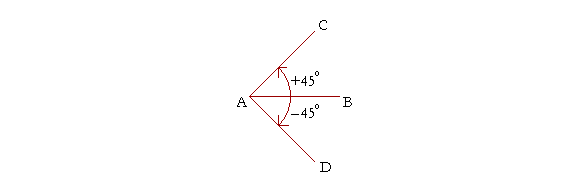
Ako završni krak rotira u suprotnom pravcu od pravca kazaljke na satu, tada kažemo da je nastali ugao pozitivan. U suprotnom kažemo da je ugao negativan.

Na slici levo su data dva ugla različito orijentisana: ugao BAC je pozitivno orijentisan i iznosi 45 (to je mera ugla i o tome govorimo u nastavku) i ugao BAD je suprotne orijentacije od ugla BAC.

Mera ugla

U ranijim matematičkim izučavanjima, stepen je bio glavna mera ugla. Prav ugao je ugao koji iznosi 90 stepeni (obeležava se 90), mera opruženog ugla je 180 i mera punog ugla je 360.

Zanimljivost: Ako ste se možda pitali zašto je ba broj 360 uzet kao mera punog kruga, a ne neki drugi broj kao na primer 100 ili 1000, odgovor je iz dva razloga. Prvo, broj 360 ima dosta delioca (2,3,4,5,6,8,...), to povlči da dele krug na delove koji se lako mogu meriti celim brojevima. Drugo, broj 360 je približno jednak broju dana u jednoj astronomskoj godini (365).

Međutim, nova mera ugla, koja se najčešće koristi u trigonometriji, je radijan. Radijan je lučna mera ugla tj. merenje radijanom je merenje lukom.

Definicija: Ako je dužina krunog luka jednaka poluprečniku tada odgovarajući centralni ugao nazivamo radijanom.

To najbolje ilustruje sledeća animacija:

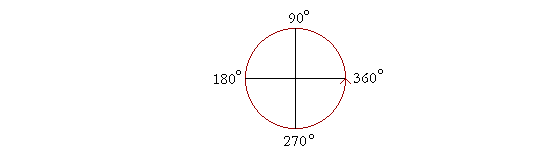
Tako na primer 180 je jednako π radijana, 90 iznosi π/2 radijana, 270 je 3π/2 radijana i konačno pun ugao je 2π radijana.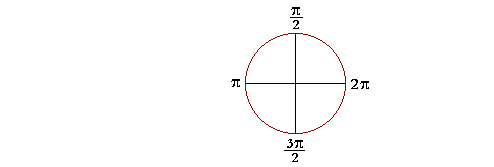

Zadatak1:

Koliko radijana iznosi ugao od 45, 60, 30?
Pogledajmo sledeće slike:

Znači, pošto je 45 = 180/4
dobijamo da je 45 = π/4 radijana.

Slično prethodnom dobijamo da je 60 = π/3 radijana i da je 30 = π/6 radijana.

Prevođenje stepena u radijan

Pošto je 1 radijan = π/180 možemo naslutiti kako izgleda formula za prevođenje stepena u radijane:
X = X * (π/180) radijana.

Primer:

120 = 120*(π/180) = (120/180)*π = (2 /3) * π = 2π/3

Prevođenje radijana u stepen

Kako je 1 = 180/π odatle je
Y radijana = Y*(180/π)

Primer:

5π/4 = (5π/4)*(180/π) = (5π*180)/4π = (5*180)/4 = 225 , ili na lakši način

5π/4 = (1+1/4)* π = π + π/4 = 180 + 45 = 225.

Domaći zadatak1:

Prevesti sledeće stepene u radijane:

a) 0 b) 270 c) 72 d)150 e) 225 f) 240

Domaći zadatak2:

Prevesti sledeće radijane u stepene:

a) π/8 b) 7π/4 c) 9π/2 d) 7π/9 e) 7π/6

Prethodna ..... Sledeća