Elementarne

trigonometrijske

funkcije
Trigonometrijske funkcije određuju vezu između dužine stranica i unutrašnjih uglova u pravouglom trouglu.

Posmatrajmo u pravouglom trouglu stranicu koja je naspram jednog od dva oštra ugla. Nazovimo takvu stranicu "naspramnom".

Sada posmatrajmo stranicu koja nije naspramna odgovarajućem posmatranom uglu, već predstavlja drugu katetu pravouglog trougla koja nije "naspramna". Tu katetu nazivamo "naleglom" za taj posmatrani ugao.

Pogledajmo sledeću sliku:


                 Slika 1.
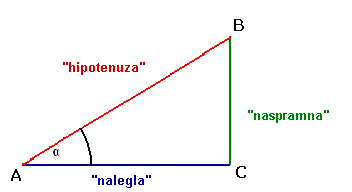
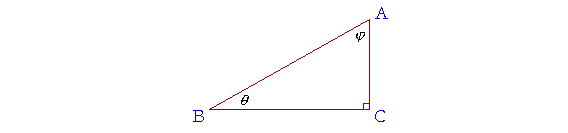
Na slici 1. prikazan je pravougli trougao ABC i označene su hipotenuza kao i "naspramna" i "nalegla" u odnosu na označeni ugao α.
Kod svakog pravouglog trougla, možemo uočiti šest različitih odnosa njegovih stranica: odnos naspramne i hipotenuze, nalegle i hipotenuze, naspramne i nalegle i tako dalje. Svaki od tih odnosa predstavlja po jednu trigonometrijsku funkciju i ima svoje istorijsko ime i skraćenicu, koja učenicima omogućava jednostavniji zapis.

Odnos naspramne stranice i hipotenuze nazivamo sinusnom funkcijom ili sinus i skraćeno zapisujemo sin.
Odnos nalegle i hipotenuze nazivamo kosinusnom funkcijom ili kosinus i skraćenica je cos.
Odnos naspramne i nalegle se naziva tangens i skraćenica je tg.

Ove tri funkcije nazivamo elementarnim trigonometrijskim funkcijama i prikazane su na sledećim slikama:



Možda ćete se pitati zašto ove odnose ne nazivamo trigonometrijskim odnosima već trigonometrijskim funkcijama. Ako pogledamo funkciju y = sin x, "ugao" x, može biti bilo koji broj. Prema tome, y = sin x je odnos između brojeva x i y , i to nije neophodno dovoditi u vezu sa geometrijom.

Preostala tri od šest odnosa stranica pravouglog trougla su: odnos hipotenuze i naspramne, odnos hipotenuze i nalegle i odnos nalegle i naspramne.

Odnos hipotenuze i naspramne stranice nazivamo kosekans i skraćeno zapisujemo csc.
Odnos hipotenuze i nalegle nazivamo sekans i skraćenica je sec.
Odnos nalegle i naspramne se naziva kotangens i skraćenica je ctg.

Pogledajmo prikaz formula opisanih funkcija na sledećim slikama:



Primetimo, da su ove funkcije, csc, sec, cot jednake recipročnoj vrednosti redom funkcija sin, cos, tan.

Zadatak1:

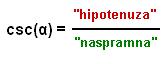
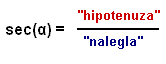
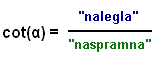
Posmatrajući datu sliku, odgovorite na sledeće pitanja:
  1. Kako se naziva stranica CA trougla ABC u odnosu na ugao θ?
  2. Kako se naziva stranica BC u odnosu na ugao θ?
  3. Kako se naziva stranica CA u odnosu na ugao φ?
  4. Kako se naziva stranica BC u odnosu na ugao φ?
Za rešenje zadatka 1. pritisnite dugme "Odgovor"!



Zadatak2:

Stranice datog trougla na slici desno se nalaze u odnosu 3:4:5. Izračunati vrednost svake od 6 trigonometijskuh funkcija, koje smo dosad naučili, u odnosu na zadati ugao θ ?.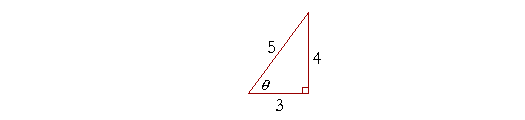
Za rešenje zadatka 2. pritisnite dugme "Odgovor"!



Zadatak3:

Neka je u pravouglom trouglu cos(α) = 3/4. Odrediti preostalih pet trigonometrijskih funkcija u odnosu na ugao α. Za rešenje zadatka 3. pritisnite dugme "Odgovor"!



Domaći zadatak1:

Koliko iznosi sinus pravog ugla?

Domaći zadatak2:

U pravouglom trouglu, stranica naspram ugla kod temena A je dužine 1. Ugao kod temena A jednak je 30. Kolika je dužina hipotenuze tog trougla? Napomena: sin(30) izračunati pomoću kalkulatora.


Formula za visinu trougla

Neka je dat proizvoljan trougao ABC i njegova visina h iz temena C na stranicu c. Ona deli stranicu c u odnosu x:(c-x) (videti sliku).



Uglovi kod temena A i B su oba oštra (Zašto?), pa možemo uočiti dva nova pravougla trougala unutar trougla ABC i unutar svakog od njih potražimo odgovarajuće odnose stranica.

Sa slike vidimo da je visina h trougla ABC naspramna stranica (u oba pravougla trougla) u odnosu na uglove kod temena A i B. Zato imamo sledeće odnose:

U pravouglom trouglu sa oštrim uglom kod temena A

x / h = cot A, a iz toga dobijamo da je x = h*cot A --------------> formula (1)

U pravouglom trouglu sa oštrim uglom kod temena B

(c-x) / h = cot B, a iz toga dobijamo da je (c - x) = h *cot B --------------> formula(2)

Iz (1) i (2), metodom zamene, dobijamo:

(c - h)*cot A = h*cot B

na osnovu ga sledi

c = h*cot A + cot B = h*(cot A + cot B).

Rešavanjem ove jednačine po h dobijamo traženu formulu za visinu trougla

h = c /(cot A + cot B).


Formula za površinu trougla

Poznato nam je da je površina bilo kog trougla jednaka jednoj polovini proizvoda stranice trougla i njoj nalegle visine. Ako posmatramo trougao ABC na sledećoj slici i ako je c stranica u odnosu na koju određujemo površinu, tada njegova površina P(ABC) biti jednaka:
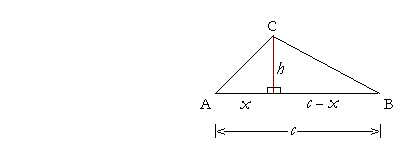
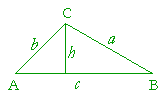
P(ABC) = 1/2 *c*h -------------------> formula (1)
Kako je sin A = h / b, dobijamo da je h = b*(sin A) -------------------> formula (2)
Ako sada u formuli (1) zamenimo h sa formulom (2), dobijamo traženu formulu za površinu trougla:

P(ABC) = 1/2*c*b*(sin A)







Prethodna ..... Sledeća