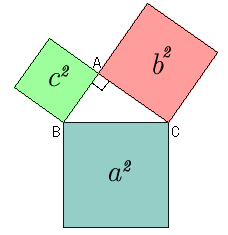
Slika 1.

 Slika 1. |
Napomena: za podsećanje šta je pravougli trougao, kliknite na dugme "pravougli trougao". |
| Kako koristimo aplet? Prvi korak: Pritiskamo dugme "Define" i time postavljamo 5 crvenih tačaka, pomoću kojih možemo prevlačiti sastavne delove velikog kvadrata nad hipotenuzom. Drugi korak: Pritiskom na željenu crvenu tačku spremni smo da određeni deo, kome ona pripada, transliramo na željeno mesto. Treći korak: Nakon prvog koraka, dugme "Define" postaje "Init" i pritiskom na njega dobijamo početni izgled animacije. |
Sada ćemo primeniti Pitagorinu teoremu za rešavanje sledećih nekoliko zadataka.
Zadatak 1:
| Kolika je površina preostalog kvadrata na datoj slici? I kolika je dužina stranica datog trougla na slici? | 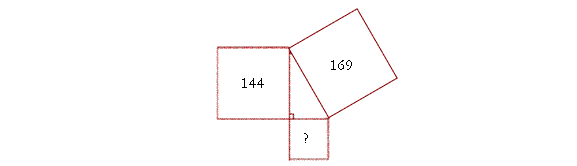
|
| Kolika je dužina nepoznate stranice x sa date slike? | 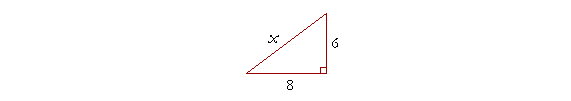
|
| Kolika je dužina nepoznate stranice x sa date slike? | 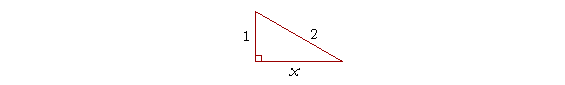
|
Ono što je takođe važno za dalje izučavanje trigonometrije jesu slični trouglovi.
Za dva trougla kažemo da su slični ako su im odgovarajući uglovi jednaki i odgovarajuće stranice proporcionalne.
U trigonometriji se vrlo često koriste dva slična trougla takva da je jedan od njih deo onog drugog, većeg trougla.
Primer2:
Trougao AEF je deo trougla ABC i oni imaju zajednički ugao kod temena A. U tom slučaju su im stranice BC i EF, koje se nalaze naspram ugla kod temena A, paralelne duži.
To nam najbolje ilustruje sledeći aplet.
| Kako koristimo aplet? Vrhom strelice miša možemo pomerati tačke obojene crveno, koje predstavljaju temena A, B i C trougla ABC. Možete primetiti da je teme E obojeno narandžastom, a teme F crnom bojom. Ukoliko vrhom strelice miša pomeramo narandžasto teme, menjamo veličinu trougla AEF, dok ukoliko vrhom strelice miša pomeramo crno teme, menjamo položaj trougla ABC. |